Sprint 2: Consensus, Medium of Exchange and Curve readthrough

Consensus Systems

A blockchain is a decentralized peer-to-peer system, and its novelty lies in decision-making (or truth verification) with no central authority - using a combination of cryptographic/mathematical proofs and economic incentives.

Coordinating nodes (computers) in a network is not unlike coordinating humans in a group to achieve an ideal, unified outcome.

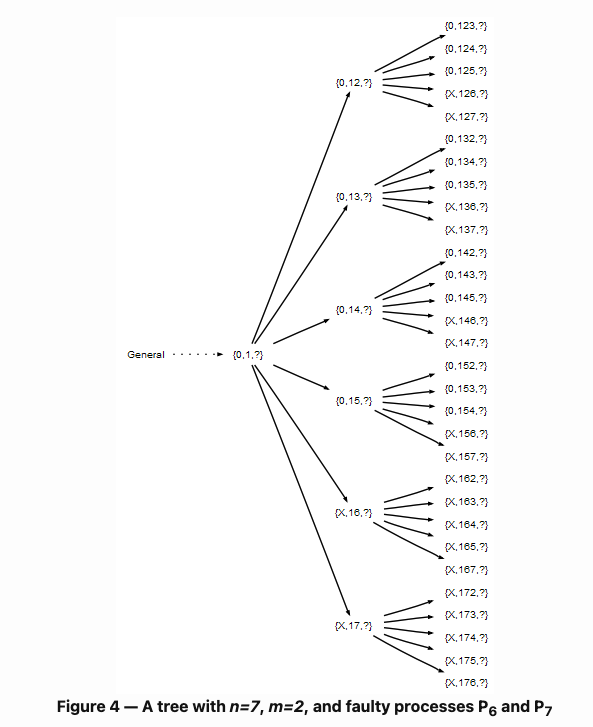
This problem is illustrated in the Byzantine Generals Problem as a group of generals coordinating a single attack-or-retreat decision - with the caveat that some of them may betray the relay of message between each other.

In a p2p payments network, that will be equivalent to nodes maliciously modifying transactions (balances, debit/credit, history etc.), being slow or simply going offline.

Nelson summarizes the Interactive Consistency conditions for a solution (i.e. Byzantine Fault-Tolerant) solution as having:

• guaranteed termination: all generals can form a decision based on the received messages
• agreement: all generals share the same final decision
• validity: all generals arrive at the same decision, which was the original and correct decision

The Lamport naive solution states that:

The problem is only solvable iff. more than two-thirds of the generals are loyal

The Bitcoin network applies BFT by using Proof-of-Work to signficantly incentivize its generals to relay the truth (since any decision will require a large investment of time and compute power / money). As long as two-thirds of the network are now relaying the truth (correct decision), the network is now secure or truthful.

Check out the rest of the Nelson that walks through the entire proof using 7 generals (1 Head General and 6 lieutenants).

Proof-of-Work, Proof-of-Stake and other consensus algorithms

BFT solutions can still differ by the underlying consensus algorith they use to build the two-thirds majority. Bitcoin and Ethereum currently use Proof of Work by incentivize truthful generals.

This piece of the solution can be innovated upon depending on the available technology or economic design of its actors.

A quick overview of different Consensus protocols by CoinDesk, and the core difference from Proof-of-Work:

• Proof of Stake: uses a stake (deposited amount) to signal influence and integrity. Bad nodes have their stake slashed.
• Proof of Activity: uses mining (cryptographic puzzle solving) to mine a block, and staking (financial ownership) to sign the block.
• Proof of Burn: incentivizes miners to burn its reward tokens for a higher chance to be reselected for mining new rewards.
• Proof of Capacity: uses storage capacity, instead of compute power, to select miners.
• Proof of Elasped Time: produces blocks in random lottery using an isolated execution environment in a processor - which guarantees integrating and confidentialy of data. This departs from the economic incentive design of the other consensus algorithms.

In 2021, Proof-of-Stake is growing in adoption due to the expansion of crypto networks (more transactions) and the limitations of today’s machines in terms of costs and computation. PoS is already deployed by major, high-TVL networks such as Polygon/Matic, Solana, Terra and Thor’s Tendermint - aside from the upcoming Ethereum 2.0’s Casper protocol

The discussion on PoW v. PoS is still ongoing, but I found this thread useful for some numbers and to add more layers to the mental model.

Crypto economy: Scarcity & Value, Mises Regression Theorem

El Salvador passed Bitcoin as legal tender, requiring all market participants to accept payments and pay taxes in BTC. This raised the question again: is Bitcoin money?

The Mises Regression Theorem discusses the emergence of a medium of exchange as:

a good with objective value from its own direct use, that later becomes subjectively valued as a function in indirect exchange.

The theorem is refuted if a money emerges without prior objective value, regardless if it was tangible or unintangible in form.

The crux of the theorem stipulates:

The subjective exchange value of money (to hold) today takes place using, as a starting point, the objective exchange values of yesterday.

A new medium of exchange emerges from:

1. A pure barter economy, which the medium has a previous direct use, or
2. An existing money-price structure, or a memory of one.

Regardless of its tangibility. In this sense, while it is a non-fiat medium of exchange, Bitcoin does not invalidate the Regression Theorem.

The price or value of Bitcoin has been modelled most popularly by its scarcity over time e.g PlanB’s Stock-to-Flow model. It is still being validated - and I also recommend reading the counter-argument by Strix Leviathan

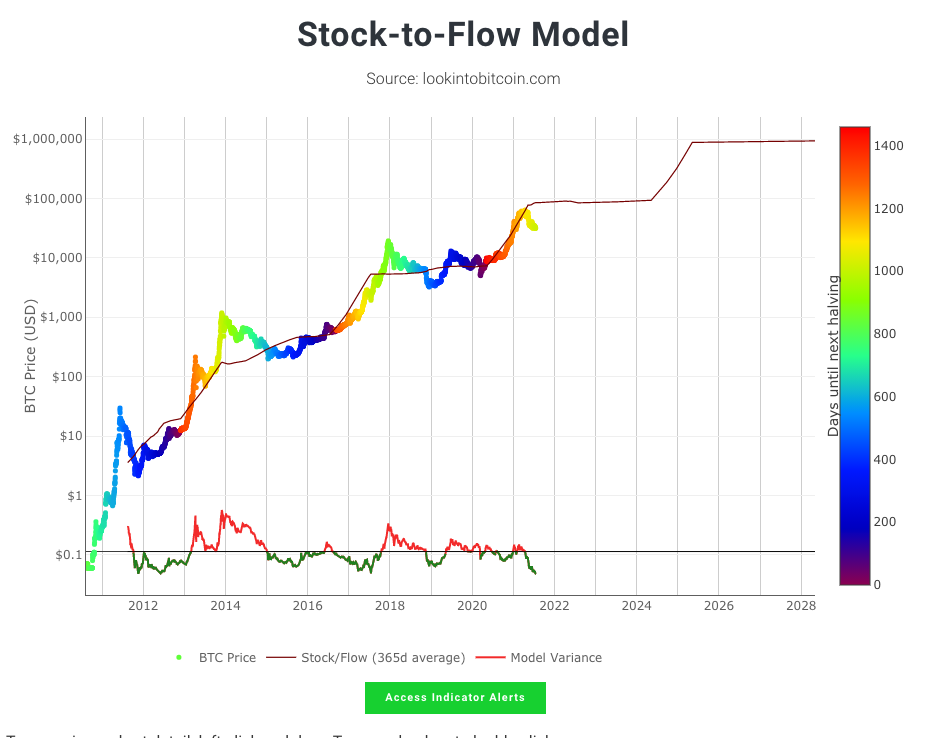
Access the realtime chart at lookintobitcoin.com

A Look into Curve Finance models

Curve (curve.fi) is an automated market maker (AMM) specializing in stable or strongly correlated token pairs. AMMs provide liquidity in electronic markets using liquidity pools and manage the relationship between pool assets using algorithms e.g. LMSR, Bayesian etc.

A subset of these AMMs use constant functions - the constant being overall reserve - and are thus called Constant Function Market Makers (CFMM). Examples of CFMMs in DeFi are Bancor, Uniswap V2 (constant product: x*y=k) and Balancer (constant mean of more than 2 assets in a pool: (x*y*z)^1/n=k).

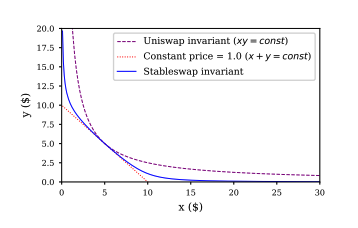
The Stableswap Invariant

Curve (v1) uses a hybrid of Constant Product and Constant Sum known as the Stableswap invariant to significantly reduce price slippage by working as a constant-sum (low slippage) function over a target x:y price range, and a constant-product (high-slippage) function at the edges.

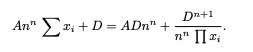
There are two particular parameters from the math in the paper:

• D being the total amount of coins at equal prices
• constant A being an Amplification coefficient

which are related by a dimensionless, dynamic leverage X (chi).

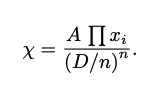
When coins are added into the pool, the new value of D is calculated. When coins are swapped within the pool, the exchange is determined by converging into D or the target coin with all other variables fixed.

The constant A is manually updated by the DAO or pool manager. A large value of A will result in all tokens being a strict 1:1 swap with no slippage. In other words, it is optimized to flatten or curve the stableswap invariant depending on the stability/pegging of one asset to the other.

Taking a look at some curve pools in July 2021:

• Largest stablecoins DAI+USDC+USDT (3pool): A=2000
• Ironbank stablecoins DAI+USDC+USDT (held reserves for the Iron Bank): A=600
• Wrapped BTC pools renBTC+wBTC+sBTC: `A=100
• Lido staked ETH pools ETH+stETH: A=50

Curve V2: AMM with Dynamic Peg

In June, Curve introduced a new AMM invariant - called CurveCrypto invariant_ for non-pegged assets (currently BTC-ETH-USD/DAI), which is still a hybrid function that does not use a pure constant-product or constant-mean function.

The CurveCrypto invariant derives from the Stableswap invariant, except it introduces a secondary parameter γ (gamma) in the definition of leverage X (chi) - re-written as K in this paper.

γ is a positive, small number representing the distance between multple constant product curves, seemingly larger at 1:1 x:y exchanges, and converges to 0 at larger values of x or y.

Similarly to the stableswap methodology, any change in tokens is optimized to cnverge on the parameter D for different fixed values of A and now γ, ranging between vales of 1E-18 ~ 1E-2 for a D value of 0.1 ~ 10E15.

Given that the CurveCrypto invariant supports unrelated assets with dynamic pegging, there is a need to separately measure profits/losses using a profit function, expressed as Xcp.

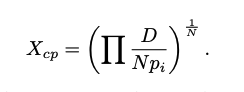
The profit/loss is determined by the variable p, which is an internal set of price scale coefficients for the balances of each token in the pool based on an internal price oracle.

The current values are available in the pool stats as well:

Essentially, values of A and γ are tested to converge D, resulting in different profit/loss margins expressed by the profit function. The combination of A, γ is selected for the highest profit margins.

That’s my understanding of Curve’s stable and dynamic-peg invariants. I haven’t seen a written update on the CurveCrypto performance so far, but it is definitely a novel take on hybrid function MMs.

I do wish the code was more decomposed though, which would make it more readable.

A Call to Cryptographic Arms

Reflecting once again on why we do what we do, I thought it would be worth citing the following from Julian Assange’s Cypherpunks: Freedom and the Future of the Internet, written in 2012, recently re-read at the Bitcoin 2021 conference.

The Wikileaks resistance is directly in opposition with the US military and government, but the cypherpunk movement is re-envisioning the web of trust underpinning the global exchange of information that is the Internet. It is a truth that will succeed the majority of this living generation, but the challenge over the next century for the layperson to deconstruct and to understand it starts now.

Cryptography pits systemic power against the laws of physics and mathematics. That is the future of the cypherpunks.

To support the Assange Defense Fund, refer to the WikiLeaks official page: HERE